Kmeans¶
DBSCAN( Density-Based Spatial Clustering of Applications with Noise)
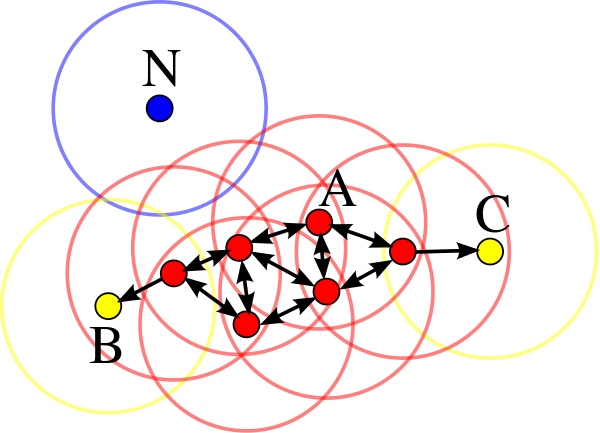
DBSCAN 需要两个参数距离ε (eps) 和形成高密度区域所需要的最少点数 (minPts)，它由一个任意未被访问的点开始，然后探索这个点的 ε-邻域，如果 ε-邻域里有足够的点，则建立一个新的聚类，否则这个点被标签为杂音。注意这个点之后可能被发现在其它点的 ε-邻域里，而该 ε-邻域可能有足够的点届时这个点会被加入该聚类中。如果一个点位于一个聚类的密集区域里，它的 ε-邻域里的点也属于该聚类，当这些新的点被加进聚类后，如果它(们)也在密集区域里，它(们)的 ε-邻域里的点也会被加进聚类里。这个过程将一直重复，直至不能再加进更多的点为止，这样，一个密度连结的聚类被完整地找出来。然后，一个未曾被访问的点将被探索，从而发现一个新的聚类或杂音。DBSCAN 可以找出任何形状的聚类，甚至能找出一个聚类，它包围但不连接另一个聚类，另外，由于 MinPts 参数，single-link effect （不同聚类以一点或极幼的线相连而被当成一个聚类）能有效地被避免。
- 核心点 如果一个点 p 在距离 ε 范围内有至少 minPts 个点(包括自己)，则这个点被称为核心点
- 可达点 点 B 和点 C 不是核心点，但它们可由 A 经其他核心点可达，所以也属于同一个聚类。
- 局外点 点 N 是局外点，它既不是核心点，又不由其他点可达
BIRCH（Balanced Iterative ReducingandClustering using Hierarchies）
针对层次聚类不适于解决大量数据的问题，Zhang 等人提出了一种基于聚类特征树（Clustering Feature Tree）的层次聚类算法：BIRCH算法（Balanced Iterative Reducing and Clustering Using Hierarchies）。BIRCH算法实现了只需要一次对数据集的遍历就可以完成聚类。其聚类的主要过程就是将所有数据依次插入构建聚类特征树的过程，而树上的每一个节点所包含的数据构成了一个对应的聚类簇。同时对于包含数据极少的节点我们可以认为它是异常点从而进行去除。
CURE （ Clustering Using Representative）
不同于一个质心或者单个点来代表一个类，CURE 算法中每个簇有多个代表点，这使得 CURE算法可以适应非球形的几何形状。CURE 算法还通过“收缩因子”减少离群点对聚类效果的影响。
- 代表点的选取
- 首先选择簇中距离质心最远的点做为第一个点
- 然后依次选择距离已选到的点最远的点
- 直到选到c 个点为止，这些点尽量得分散，捕获了簇的形状和大小
ROCK （RObust Clustering using linKs）
A Hierarchical ClusteringAlgorithm for Categorical Attributes主要用在categorical的数据类型上；
Chameleon1¶
（A Hierarchical Clustering AlgorithmUsing Dynamic Modeling）Chameleon，变色龙算法。算法如其名，它可以自动地、适应地合并簇，对各种奇葩的形状也能应对自如。
它里用到的linkage是kNN（k-nearest-neighbor）算法， K-NN是一种基于实例的学习，或者是局部近似和将所有计算推迟到分类之后的惰性学习。k-近邻算法是所有的机器学习算法中最简 单的之一。无论是分类还是回归，衡量邻居的权重都非常有用，使较近邻居的权重比较远邻居的权重大。例如，一种常见的加权 方案是给每个邻居权重赋值为1/ d，其中d是到邻居的距离。邻居都取自一组已经正确分类（在回归的情况下，指属性值正确）的对象。虽然没要求明确的训练步骤，但这也可以当作是此算法的一个训练样本集。k-nn算法的缺点是对数据的局部结构非常敏感。并以linkage构建一个graph.
Chameleon使用hMetis算法根据最小化截断的边的权重之和来分隔k近邻图。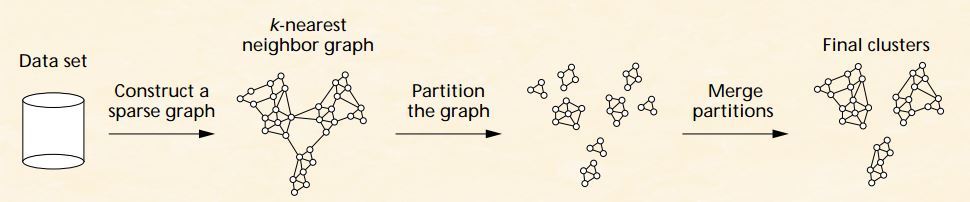
Chameleon的聚类效果被认为非常强大，比BIRCH好用，但运算复杂度很高，O(n^2)。它是由George Karypis 教授提出的一种基于动态建模（Dynamic modeling）思想的层次聚类算法。该算法通过计算两个聚类簇之间的相似度和互连性从而克服CURE和ROCK等算法的缺点。变色龙算法首先将所有的数据根据他们之间的距离划分成众多的小的簇，通过计算相近簇之间的相似度和互连性不断合并形成大的聚类簇。
R操作¶
标准化数据矩阵¶
在R里面我用scale标准化，每次scale只能读取处理标准化dataframe数据的一列， read.csv加载进来的数据就是dataframe类型，然而scale处理的是numeric matric对象。
怎么把dataframe类型转为matric类型呢，用
data<-data.matrix(data)
data_scale<-scale(data)
scale(x, center = TRUE, scale = TRUE)
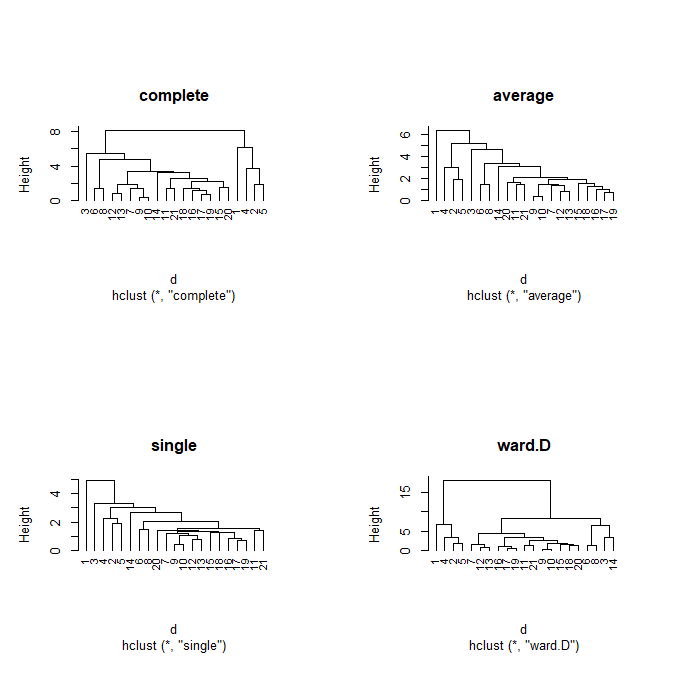
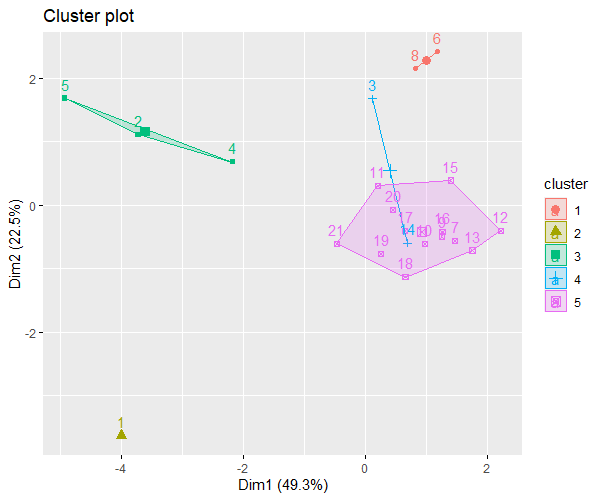kmeans
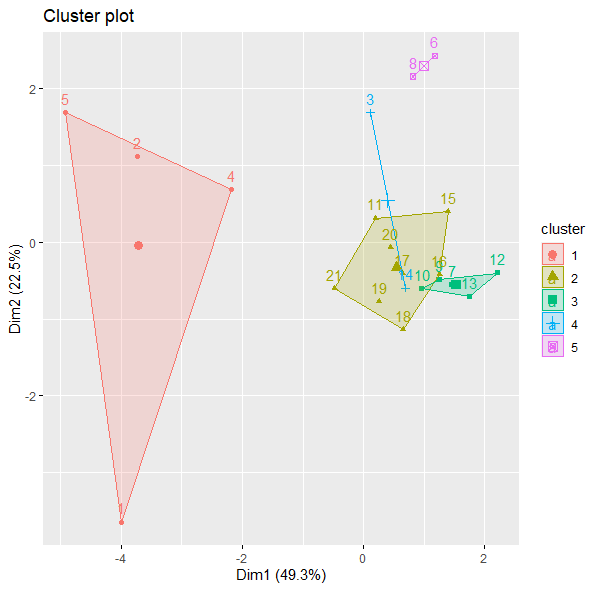DBSCAN